Posiciones del átomo, planos cristalográficos y direcciones en la estructura cristalina HCP

¡Hola de nuevo!

Hoy volvemos con un tema que puede parecer bastante confuso pero es realmente muy simple: cómo ubicar posiciones de átomos, planos cristalográficos y direcciones en la celda unitaria de una estructura cristalina HCP.

Y es que para muchos de nosotros que carecemos de visión espacial, o no recordamos mucho de nuestras clases de geometría descriptiva, ubicarnos en un cubo ya cuesta bastante ¡imagínense un prisma hexagonal! Esperamos que este tutorial les sea, como a nosotros, de mucha ayuda.

¿Por dónde comenzamos?

Ejes cristalográficos utilizados para las celdas unitarias HCP

.

¡Por nuestro sistema de referencia!

Análogamente a como hacemos en las celdas cúbicas, usaremos ejes de referencia para ubicar posiciones, direcciones y planos cristalográficos en la celda unitaria HCP. A diferencia de las celdillas cúbicas, como la BCC y la FCC, la celdilla HCP emplea un sistema de referencia de cuatro ejes que consta de:

• Tres ejes, a1, a2 y a3, situados en un plano basal --la cara inferior del prisma hexagonal está asentada sobre él--, denominados ejes basales que forman ángulos de 120° entre sí (tomemos como ejemplo la separación entre + y +a3).
• Un eje, llamado c, que es perpendicular al plano basal. 

¿Cómo determinamos una posición en la celda unitaria HCP?

Para comenzar, debemos tener en cuenta algunas consideraciones:

• Las posiciones, como en las celdillas cúbicas, se escriben entre paréntesis y separadas por coma.  Por convención,los tres primeros índices corresponden a las proyecciones a lo largo de los ejes del plano basal, a1, a2 y a3 (Callister, 2005). 

•  Para mantener la uniformidad entre las direcciones y los planos de la celdilla unitaria HCP, se ha acordado que:

Con base en todo lo anterior, procedamos a determinar la posición del átomo señalado en la siguiente figura:

Extraído de Ingeniería de Materiales. Unidad 3. Direcciones y Planos en Celdas Hexagonales. Universidad Politécnica de Valencia. Disponible en: https://www.youtube.com/watch?v=XiGtY62FM78

• Como es una celda unitaria, la distancia desde el origen hasta los puntos donde el prisma intersecta los ejes es igual a la unidad. 

• Luego, si nos movemos por el eje a1 y a través del lado del prisma que conecta a +a1 con -a2, podemos ver que para la posición a1, el átomo está en 1. 

• Análogamente, si nos movemos por el eje a3 y a través del lado del prisma que conecta +a3 con -a2, para la posición a2, el átomo está en 1.

• Sabemos que el átomo está sobre la parte negativa del eje a2.  Usaremos entonces la relación entre los tres ejes basales de la siguiente manera:

• Finalmente, el átomo está en el plano basal superior (cara superior del prisma), por lo que su posición en el eje c es 1. 

Así, tenemos que la posición del átomo en la celda unitaria es la siguiente:

Ejercicios

Extraído de Ingeniería de Materiales. Unidad 3. Direcciones y Planos en Celdas Hexagonales. Universidad Politécnica de Valencia. Disponible en: https://www.youtube.com/watch?v=XiGtY62FM78

 Veamos los átomos verde y rojo de la figura:

Para el átomo rojo:

• Si nos movemos a través del lado del vértice que une a +a2 con -a1, podemos observar que para la posición a1, el átomo está en -1.
• Si cruzamos el lado del vértice que une a -a3 con +a2, tendremos que para la posición a3, el átomo está en -1.
• Usando la relación de uniformidad, obtendremos que la coordenada del átomo sobre el eje a2 es igual a 2. 
• Como el átomo está en el plano basal inferior (cara inferior del prisma hexagonal), la coordenada del átomo sobre el eje c es 0. 

Así, la posición del átomo es:

Vamos ahora con el atomo verde:

• Si nos movemos a través de la arista que conecta a +a2 con -a1, tendremos que la posición sobre el eje a2 es 1.
• Desplazándonos por la arista que conecta a +a3 con -a1, la posición sobre el eje a3 es 1. 
• Usando la relación de uniformidad, obtendremos que la coordenada del átomo sobre el eje a1 es igual a -2. 
• El átomo se encuentra sobre la cara superior del prisma hexagonal, por lo que su posición en el eje c es 1. 

Así, la posición del átomo es:

Índices de dirección en celdas unitarias HCP

¡Recordemos...!

"Los índices de las direcciones cristalográficas son los componentes de un vector dirección descompuesto sobre cada eje ordenado y reducidos a mínimos enteros. 

Para indicar en forma gráfica una dirección en una celda unitaria, se dibuja un vector de dirección desde un origen, que generalmente es un vértice de la celda, hasta que emerge a la superficie del cubo.  Las coordenadas de posición de la celda unidad donde el vector dirección emerge de la superficie del cubo después de convertirlas en enteros son los índices de dirección." (Smith, 2004)

Como en las celdillas unitarias cúbicas, los índices de dirección se indican entre corchetes, sin comas y con una barra encima de los números negativos.

 

En este caso, los ínices u, v y t  son las componentes del vector en las direcciones de los ejes a1, a2 y a3 respectivamente. El índice w es la componente que se encuentra sobre el eje c. 

Para mantener la uniformidad entre las direcciones y los planos HCP se ha acordado para las direcciones que:

El procedimiento para ubicar direcciones en las celdas HCP es esencialmente el mismo que en las celdillas unitarias cúbicas, sólo que usando cuatro ejes en vez de tres y tomando en cuenta la consideración de uniformidad. Entonces:

• Escogemos un origen.
• Trazamos un vector desde el origen hasta la superficie del cubo. 
• Determinamos las coordenadas de posición de los extremos y efectuamos la resta de las coordenadas de la punta del vector (hacia donde vamos) menos las coordenadas de la cola del vector (de donde venimos). 
• Convertimos las coordenadas resultantes a los mínimos enteros. 
• Encerramos los mínimos enteros entre corchetes y de haber uno con signo negativo, sustituimos la notación habitual por una barra encima del número.

 Veamos un ejemplo: 

Extraído de Ingeniería de Materiales. Unidad 3. Direcciones y Planos en Celdas Hexagonales. Universidad Politécnica de Valencia. Disponible en: https://www.youtube.com/watch?v=XiGtY62FM78

En este caso el vector dirección ya está trazado, por lo que solo hallaremos sus índices. 

• La cola del vector está en el origen de los ejes ordenados, de coordenadas (0, 0, 0, 0). 
• La punta del vector está en el punto (-1, -1, 2, 1). 
• Al restar la punta menos la cola nos quedan las coordenadas (-1, -1, 2, 1).
• Todos los números son enteros, así que no tenemos que reducir a mínimos enteros. 
 

Por lo tanto, los índices de dirección del vector son:

Ejercicios

Extraído de Ingeniería de Materiales. Unidad 3. Direcciones y Planos en Celdas Hexagonales. Universidad Politécnica de Valencia. Disponible en: https://www.youtube.com/watch?v=XiGtY62FM78

Tenemos las siguientes direcciones:

Ya hemos hecho la dirección verde. Tomemos ahora la roja:

• El vector parte desde el origen de coordenadas, por lo que las coordenadas de su cola son (0, 0, 0, 0). 
• La punta del vector se encuentra en el punto (1, 1, -2, 1).
• Si efectuamos la resta de las coordenadas de la punta menos la cola tendremos las coordenadas (1, 1, -2, 1). Nuevamente, todas las coordenadas son números enteros, por lo que no tenemos que reducir a mínimos enteros. 

Así, los índices de dirección del vector dirección rojo son:

Vamos ahora con la dirección azul:

• La cola del vector está en el punto (0, 0, 0, 0).
• La punta del vector está en el punto (-1, 2, -1, 0).
• La resta de las coordenadas de la base menos la punta arroja las coordenadas (-1, 2, -1, 0). Los números son enteros y por ende nos ahorramos la reducción a mínimos enteros.

Los índices de dirección del vector dirección azul son:

 Para finalizar con las direcciones, encontremos los índices para el vector de la imagen:

• La cola del vector está ubicada en el punto (2, -1, -1, 1).
• La punta del vector está ubicada en el punto (1, -2, 1, 1).
• La resta de la punta menos la cola del vector da las coordenadas (-1, -1, 2, 0). Todos los valores son enteros, por lo que no debemos reducirlos a mínimos enteros. 

Los índices de dirección del vector son: 

Índices de Miller-Bravais para planos cristalográficos en celdas unitarias HCP

¡Recordemos...!

"Los índices de Miller de un plano cristalino se definen como el recíproco de las fracciones de intersección (con fracciones simplificadas) que el plano presenta con los ejes cristalográficos" (Smith, 2005).

¿Qué significa esto?

Los índices de Miller nos proporcionan información sobre la ubicación y orientación de planos cristalográficos específicos que cortan nuestra celdilla unitaria. Para determinar los índices de Miller de un plano, primero encontramos las intersecciones de nuestro plano de interés con los ejes ordenados y los recíprocos de dichas intersecciones, obtenidos al invertirlas y llevarlas a mínimos enteros (de ser fracciones), son los índices deseados.

De forma similar a las celdas unitarias cúbicas, en la celda unitaria HCP las aristas "representan longitudes unidad y las intersecciones de los planos reticulares se miden con base en estas longitudes unidad" (Smith, 2005).

Como en las celdillas cúbicas, dos planos paralelos tienen los mismos índices de Miller-Bravais.

Como en el caso de los índices de dirección, el procedimiento para enontrar los índices de Miller-Bravais de un plano cristalográfico dado en una celda unitaria HCP es idéntico al usado para una celdilla cúbica:

• Primero elegimos un origen por el que no pase el plano de interés. 
• Determinamos las intersecciones del plano con los ejes ordenados. 
• Luego, invertimos las intersecciones para hallar sus recíprocos. 
• Si hay fracciones, llevamos los recíprocos a los mínimos enteros. Los números resultantes son los índices de Miller-Bravais del plano y se representan de la siguiente forma: 

Donde h es el recíproco de la intersección con el eje a1, k es el recíproco de la intersección con el eje a2, i el de la intersección con el eje a3 y l con el eje c. Nuevamente, si hay un número negativo se sustituye la notación tradicional por una barra encima del número. 

Ejercicios

Extraído de Ciencias e Ingeniería de Materiales, 3era ed. Smith, William. McGraw-Hill.

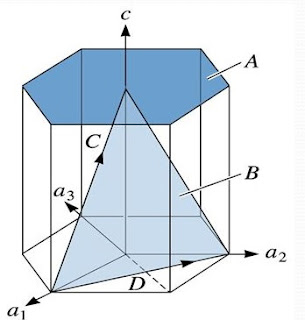
Veamos los planos de la figura a:

Para el plano a:

• Si vemos la orientación del plano, notaremos que es paralelo al eje a1 y al eje c, por lo tanto, su intersección con estos es en el infinito. 
• La intersección con el eje a2 se produce en -1. 
• El plano intersecta a a3 en 1. 

Para el plano b:

• El plano intersecta al eje a1 en 1. 
• El plano b es paralelo al eje ordenado a2, por lo que la intersección con este se produce en el infinito. 
• La intersección con el plano a3 está en -1. 
•  La intersección con el plano c está en 1/2.

Para el plano c:

Podemos observar en la figura que el plano c es paralelo al plano contenido en la cara vertical del prisma hexagonal que está entre los ejes -a1 y +a2. Como mencionamos arriba, dos planos paralelos tienen los mismos índices de Miller-Bravais, por lo que procederemos con el plano apoyado en la cara del prisma: 

• La intersección con a1 está en -1.
• La intersección con a2 está en 1. 
• El plano es paralelo a los ejes a3 y c, por lo que los intersecta en el infinito. 

 Las intersecciones, recíprocos e índices de Miller-Bravais para cada plano señalado pueden verse en la siguiente tabla:

¿Dudas?

Si eres más visual y consideras que lo entenderías mejor con un video, acá te dejamos uno que explica muy bien cómo encontrar los índices de Miller-Bravais para planos:

El profesor Dr. David García Sanoguera explica los tres tópicos en este video:

Actualizaremos esta publicación en cuanto consigamos un video que explique bien la ubicación de posiciones y direcciones en las celdas unitarias hexagonales compactas.

Bibliografía

• Callister, W. (2005).  Introducción a la Ciencia e Ingeniería de Materiales. Editorial Reverté. Barcelona, España. 
• Smith, W. (2004). Ciencia e Ingeniería de Materiales 3era edición. McGraw-Hill. Madrid, España.