Densidades atómicas en celdas unitarias
Hoy traemos tres conceptos que pueden resultar de interés a los estudiantes de las Ciencias de los Materiales. Estos corresponden a las densidades atómicas volumétrica, planar y lineal de las celdas unitarias cúbicas.
¡Recordemos que...!
La mayoría de los metales son sólidos cristalinos, es decir, los átomos que los conforman están ordenados en una disposición -o patrón- que se repite a lo largo del cuerpo de dichos sólidos. Este ordenamiento atómico recibe el nombre de estructura cristalina.
La mayoría de los metales son sólidos cristalinos, es decir, los átomos que los conforman están ordenados en una disposición -o patrón- que se repite a lo largo del cuerpo de dichos sólidos. Este ordenamiento atómico recibe el nombre de estructura cristalina.
Si consideramos a los átomos del metal como esferas rígidas, y que estas esferas se sitúan en las intersecciones de tres familias de planos fomadas por una infinita cantidad de planos paralelos y equidistantes (Fernández, Fernández y Fidalgo, 2016) tenemos entonces que estos puntos de intersección forman una red puntual tridimensional, también llamada red espacial o red cristalina.
Las redes tienen la característica de que todos sus puntos tienen el mismo entorno; es decir, la disposición de los átomos en el sólido es uniforme. La celda unitaria es la mínima unidad estructural repetida que contiene todos los elementos de simetría del cristal.
 |
| a) Red espacial de un sólido cristalino ideal b) celda unitaria mostrando las constantes de red. |
Ya que recordamos qué es una celda unitaria, pasemos al cálculo de las tres densidades atómicas asociadas a ella.
Densidad volumétrica
Sabemos que en una celda unitaria, el factor de empaquetamiento atómico nos proporciona una relación del volumen que ocupan los átomos dentro de ella. Sabemos también que la densidad de un material es una función de la masa que este posea y el volumen que ocupe.
Ahora bien, aunque la densidad depende de los tamaños de los átomos o iones que forman el material, el "tamaño atómico no cambia mucho al pasar de los elementos ligeros a los elementos pesados" (Mangonon, 2001). Esto quiere decir, que el volumen atómico es aproximadamente el mismo y por tanto, el factor de empaquetamiento no es indicador suficiente para la densidad de un material. Sin embargo, la masa atómica sí que varía entre los distintos elementos, siendo los metales más pesados que elementos como el carbono y el hidrógeno, entre otros.
Es aquí donde entra la utilidad de la densidad volumétrica, que es la relación entre la masa de los átomos contenidos en la celda unitaria y el volumen de dicha celda.
Si mantenemos el supuesto de átomos esféricos y rígidos para la estructura cristalina de la celda unitaria de un metal, y obtenemos el valor del radio atómico a través de un análisis de difracción de rayos x podemos conocer la densidad volumétrica del metal a través de la siguiente ecuación:
Que se traduce en:
Donde:
Ejemplo
Extraído de Ciencias e Ingeniería de Materiales, 3era ed (pp. 61). Smith, William. McGraw-Hill.
El cobre tiene una estructura cristalina FCC y un radio atómico de 0,1278 nm. Considerando los átomos como esferas rígidas que se tocan entre sí a lo largo de la diagonal de la celda unidad FC como se muestra en la figura, calcue el valor teórico de la densidad del cobre en megagramos por metro cúbico. La masa atómica del cobe es de 63,54 g/mol.
En la figura se muestra la relación entre la longitud de un lado de la celdilla (a) y el radio atómico (R). Si despejamos a de la expresión obtenemos:
- n: Número de átomos en la celda.
- M: Masa atómica.
- Vc: Volumen de la celda unitaria.
- NA: Número de Avogadro (6,023*10^23 átomos/mol). Como veremos en el ejemplo, se divide el numerador entre el número de Avogadro para eliminar las unidades de átomos/mol que quedan de multiplicar el número de átomos por la masa atómica.
Ejemplo
Extraído de Ciencias e Ingeniería de Materiales, 3era ed (pp. 61). Smith, William. McGraw-Hill.
El cobre tiene una estructura cristalina FCC y un radio atómico de 0,1278 nm. Considerando los átomos como esferas rígidas que se tocan entre sí a lo largo de la diagonal de la celda unidad FC como se muestra en la figura, calcue el valor teórico de la densidad del cobre en megagramos por metro cúbico. La masa atómica del cobe es de 63,54 g/mol.
En la figura se muestra la relación entre la longitud de un lado de la celdilla (a) y el radio atómico (R). Si despejamos a de la expresión obtenemos:
En la celda unidad FCC hay cuatro átomos por celda unidad. Cada átomo de cobre tiene una masa de:
El volumen de la celda unidad del cobre (Cu) es:
Así, la densidad del cobre es:
Densidad atómica planar
Se utiliza para calcular la densidad atómica en planos cristalográficos, utilizando la relación entre el número de átomos cortados por la superficie de interés y el área de dicha superficie. A esta relación se le denomina densidad atómica planar.
De manera más sencilla, la densidad planar es "la fracción del área del plano cristalográfico ocupada por átomos (representados como círculos)" (Callister, 2005).
Esta magnitud es calculada a través de la siguiente ecuación:
Para la utilización de esta ecuación hay que tomar en cuenta un par de factores:
- Debe utilizarse el área de un plano que corte a la celda unidad.
- Para que el área de un átomo se contabilice, el plano cristalográfico de interés debe cortar el centro del átomo.
Ejemplo
Calcule la densidad atómica planar en el plano (110) de la red BCC del hierro alfa en átomos por milímetro cuadrado. La constante de red del hierro alfa es 0,287 nm.
 | ||
| A la izquierda: Celda unitaria de posiciones atómica BCC mostrando un plano en (110) sombreado. A la derecha: Áreas de los átomos en la celda unitaria BCC cortadas por el plano (110). |
El número equivalente de átomos cortados por el plano (110) en términos de área dentro de la celda unitaria BCC es:
- Centro: 1 átomo.
- 4 esquinas: 1/4 de átomo.
- Total: 1+4(1/4) = 2 átomos.
Así, la densidad planar es:
Densidad atómica lineal
Corresponde a la fracción de longitud de línea, de una dirección cristalográfica particular, que pasa a través de los centros de los átomos. Es importanto porque en ocasiones resulta necesario determinar la cantidad de átomos que se encuentran sobre varias direcciones cristalográficas en las estructuras cristalinas.
La densidad atómica lineal se calcula a través de la siguiente ecuación:
Entendiéndose que la longitud selecciona se encuentra contenida en la celda unitaria. Repasemos el concepto con un ejemplo.
Ejemplo
Extraído de Ciencias e Ingeniería de Materiales, 3era ed (pp. 63). Smith, William. McGraw-Hill.
Calcule la densidad atómica lineal en la dirección [110] de la red cristalina de cobre en átomos por milímetro. El cobre es FCC y tiene una constante de red de 0,361 m.
Los átomos cuyos centros corta la dirección [110] se muestran en la figura. Se escoge como longitud de la línea la diagonal de la cara de la celda FCC. el número de diámetros atómicos cortados por esta línea es:
Ejemplo
Extraído de Ciencias e Ingeniería de Materiales, 3era ed (pp. 63). Smith, William. McGraw-Hill.
Calcule la densidad atómica lineal en la dirección [110] de la red cristalina de cobre en átomos por milímetro. El cobre es FCC y tiene una constante de red de 0,361 m.
 | |
| Diagrama para calcular la densidad atómica lineal en la dirección [110] en una celda unidad FCC. |
Los átomos cuyos centros corta la dirección [110] se muestran en la figura. Se escoge como longitud de la línea la diagonal de la cara de la celda FCC. el número de diámetros atómicos cortados por esta línea es:
- Átomo central: 1 diámetro
- 2 Átomos en las esquinas: 1/2 diámetro
- Total: 1 + 2(1/2)= 2 átomos.
¿Dudas?
Pilla este video del profesor David García Sanoguera
Bibliografía
- Callister, W. (2005). Introducción a la Ciencia e Ingeniería de Materiales. pp 49. Editorial Reverté. Barcelona, España.
- Fernández, Fernández y Fidalgo (2016). Tecnología Industrial II. pp 28. Editorial Paraninfo.
- Mangonon, P. (2011). Ciencia de Materiales: Selección y Diseño. Prentice Hall. México DF, México.
- Smith, W. (2004). Ciencia e Ingeniería de Materiales 3era edición. pp 61-63. McGraw-Hill. Madrid, España.









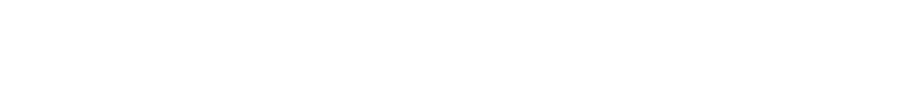


Comentarios
Publicar un comentario