Sistemas de deslizamiento en los metales
¡Hola de nuevo!
Hoy les hablaremos sobre un tema fundamental en el estudio de la deformabilidad de los metales: el deslizamiento.
En este artículo discutiremos qué es el deslizamiento, cómo se produce e introduciremos el concepto de sistemas de deslizamiento. Esperamos, como siempre, que les sea de provecho.
Comenzaremos repasando un concepto fundamental para este tema: el de las dislocaciones.
Dislocaciones
Son imperfecciones lineales o unidimensionales en el ordenamiento estructural perfecto de una red cristalina, que se producen en torno a algunos átomos desalineados. Estas surgen por dos causas: durante el proceso de solidificación del material o cuando este está asiendo deformado.
Son imperfecciones lineales o unidimensionales en el ordenamiento estructural perfecto de una red cristalina, que se producen en torno a algunos átomos desalineados. Estas surgen por dos causas: durante el proceso de solidificación del material o cuando este está asiendo deformado.
Según la forma que siga esta imperfección, las dislocaciones pueden ser de tres tipos:
Dislocación helicoidal (o de tornillo)
Tiene lugar cuando el material se deforma por una tensión de corte o cizalladura (aquella que es tangente al plano donde actúa). Como se muestra en la figura, esta dislocación puede ilustrarse en forma de un corte parcial a través de un cristal perfecto. Dicho corte se tuerce y luego se desplaza uno de sus lados sobre el otro en una distancia igual a un átomo.
Tiene lugar cuando el material se deforma por una tensión de corte o cizalladura (aquella que es tangente al plano donde actúa). Como se muestra en la figura, esta dislocación puede ilustrarse en forma de un corte parcial a través de un cristal perfecto. Dicho corte se tuerce y luego se desplaza uno de sus lados sobre el otro en una distancia igual a un átomo.
Si en un plano cristalográfico damos una revolución alrededor del eje sobre el cual el cristal fue torcido, partiendo del punto x y recorriendo espaciamientos atómicos iguales en cada dirección, terminaremos a un espacio atómico por debajo de nuestro punto de partida (punto y). Si continuáramos nuestra rotación, trazaríamos una trayectoria en espiral (de aquí el nombre). El eje alrededor del cual realizamos la revolución es la dislocación helicoidal o de tornillo. El desplazamiento de los átomos debido a esta dislocación es lineal.
Dislocación de borde (o de cuña)
El efecto que tiene esta dislocación sobre la estructura atómica
preexistente es que los átomos que se encuentren por encima de la línea
de dislocación van a comprimirse y se acercarán unos a otros, mientras
que los que se encuentren por debajo se estirarán y por ende, se
alejarán de sus posiciones de equilibrio.
Dislocaciones mixtas
Como su nombre lo indica, son una mezcla de dislocaciones de borde y helicoidales, con na zona de transición entre ambas.
Como su nombre lo indica, son una mezcla de dislocaciones de borde y helicoidales, con na zona de transición entre ambas.
Vector de Burgers
Hay un componente común para todos los tipos de dislocaciones y éste es el vector de Burgers, denotado con la letra b. Este representa la magnitud y dirección de la distorsión de la estructura cristalina que está sufriendo la dislocación y resulta de especial utilidad porque podemos conocer el tipo de dislocación a partir de las orientaciones relativas de las líneas de dislocación y por el vector de Burgers.
Para una dislocación helicoidal, el vector de Burgers es el vector requerido para cerrar la trayectoria de espiral y volver al punto inicial. La dislocación en este caso es paralela al vector.
Para una dislocación de borde, al seguir una trayectoria en círculo en
el sentido de las manecillas del reloj alrededor de la dislocación,
partiendo del punto x y recorriendo un número igual de espaciamientos
atómicos en cada dirección, finalmente nos alejaríamos un espaciamiento
atómico del punto de partida. Nuevamente, el vector necesario para cerrar el circuito y volver a nuestro punto inicial es el vector de Burgers, pero en este caso es perpendicular a la dislocación.
En dislocaciones mixtas, el vector de Burgers no es ni perpendicular ni paralelo a la dislocación.
Independientemente del tipo de dislocaciones, sin embargo, el vector de Burgers es una constante para todos los puntos a lo largo de la línea de dislocación. Así, aunque esta cambie de dirección y naturaleza dentro de un cristal, el vector de Burgers será el mismo. En metales, el vector de Burgers de una dislocación está orientado en la dirección cristalográfica más densamente empaquetada y su magnitud es igual a la distancia interplanar.
Para finalizar, debemos acotar que si bien estas imperfecciones son
defectos desde el punto de vista del arreglo perfecto de los átomos en
la estructura cristalina, no son imperfecciones del material mismo. Como
sugiere Askeland (1998), "estos 'defectos' pudieran haber sido
agregados de manera intencional, a fin de producir un conjunto deseado
de propiedades mecánicas y físicas", en este caso, la deformabilidad del material trabajado.
"Cuando se aplica una fuerza cortante en la dirección del vector de Burgers a un cristal que contenga una dislocación, ésta se puede mover al romper los enlaces entre átomos de un plano. El plano cortado se desplaza ligeramente para establecer enlaces con el plano parcial origil de átomos. Este desplazamiento hace que la dislocación se mueva un espacio de un átomo hacia el lado. Si este proceso continúa, la dislocación se recorre a través del cristal hasta que se produce un escalón en el exterior del mismo; el cristal ha sido deformado" (Askeland, fecha) plásticamente pues estos átomos no recobrarán su posición original una vez se halla detenido la fuerza.
"El proceso mediante el cual se produce la deformación plástica por el movimiento de dislocaciones se denomina deslizamiento" (Callister, 2004). Dicho movimiento se produce en respuesta a una tensión de cizalladura aplicada.
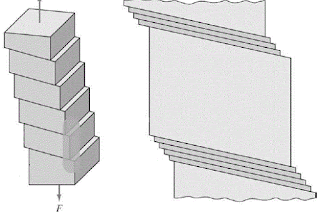
Como afirma Callister (2004), el movimiento de una dislocación es análogo al andar de una oruga. Esta estira su último par de patas igual a la distancia entre dos pares de patas, formando ua encorvadura en su cuerpo cerca de su extremo posterior. El siguiente par de patas sube y se desplaza, moviendo la encorvadura hasta alcanzar el extremo anterior. La encorvadura de la oruga y su movimiento corresponden al semiplano adicional de átomos en una deformación plástica ocasionada por una dislocación de cuña.
En la figura observamos que la dislocación de tornilla producida por una tensión cortante se manifiesta de manera distinta. Sin embargo, la deformación plástica neta resultante del movimiento de ambas dislocaciones es la misma.
Sistemas de deslizamiento
Las dislocaciones producen desplazamientos atómicos sobre planos y direcciones cristalográficas específicas, que usualmente son los de máxima compactabilidad y los más separados entre sí (Smith, 2004). Esto no es producto del azar. Las dislocaciones se mueven en los planos más empaquetados porque la tensión cortante necesaria para desplazar los átomos es menor que en los planos menos empaquetados.
Sin embargo, existen algunas excepciones. Si el desplazamiento sobre un plano densamente empaquetado está restringido, los planos de menor empaquetamiento pueden activarse.
Asimismo, las direcciones favorecidas para el deslizamiento son aquellas con mayor fracción de empaquetamiento lineal porque la energía necesaria para mover átomos de una posición a otra es menor cuando los átomos se encuentran más cerca los unos de los otros.
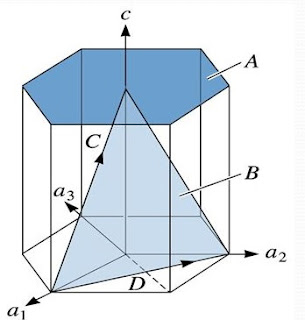
Estos planos y direcciones favorecidas se denominan planos y direcciones de deslizamiento y la combinación de un plano de deslizamiento con una dirección de delizamiento es llamado sistema de deslizamiento.
El sistema de deslizamiento depende de la estructura cristalina de los metales y es tal que la distorsión atómica que acompaña al movimiento de una dislocación es mínima. Para los metales, existen sistemas de deslizamiento característicos de cada estructura cristalina. Estos se presentan en la siguiente tabla:
 |
| Extraído de Ciencia e Ingeniería de Materiales 3era edición. McGraw-Hill. Smith, William. McGraw-Hill. Madrid, España. |
- Askeland, D. (1998) Ciencia e Ingeniería de los Materiales 3era edición. International Thomson Editores. México, México.
- Callister, W. (2005). Introducción a la Ciencia e Ingeniería de Materiales. Editorial Reverté. Barcelona, España.
- Smith, W. (2004). Ciencia e Ingeniería de Materiales 3era edición. McGraw-Hill. Madrid, España.






Comentarios
Publicar un comentario